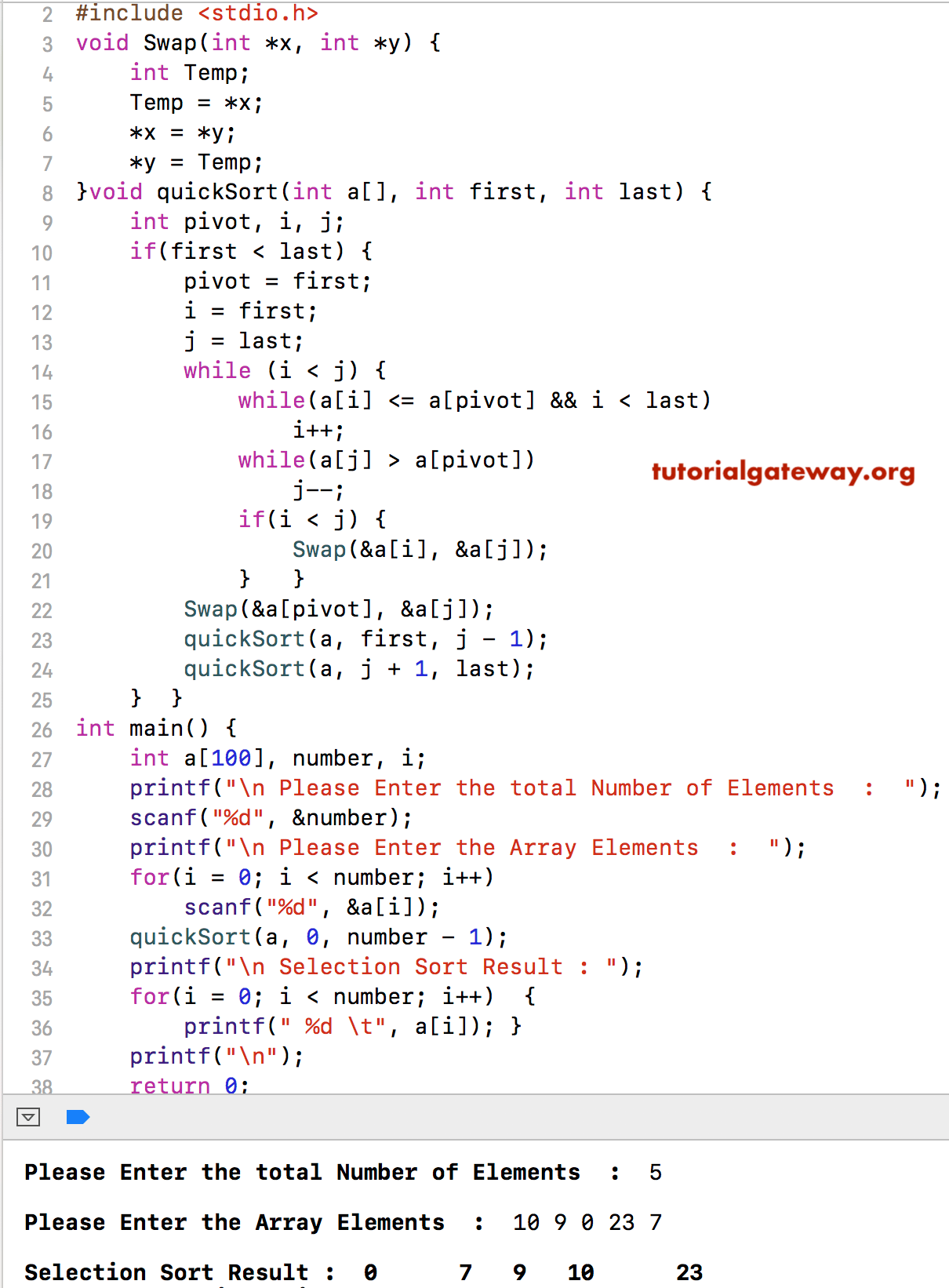
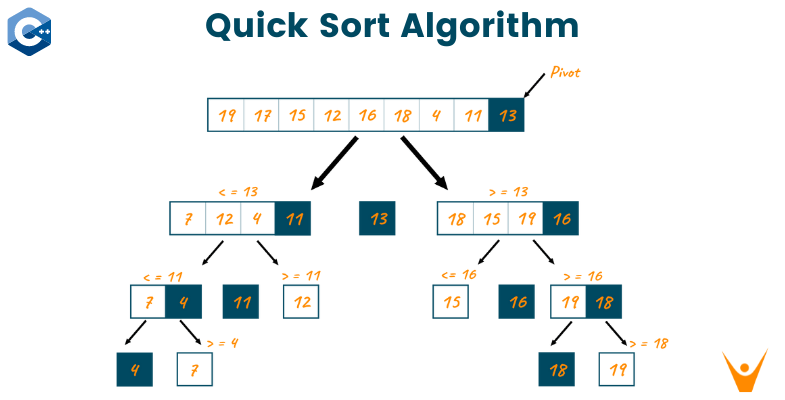
Okay, so I decided to get my hands dirty with quick sort in C the other day. Been a while since I messed with sorting algorithms directly, and I figured, why not start with quick sort? People say it’s efficient, though maybe not the simplest to grasp initially.
Getting Started
First thing, I fired up my usual simple code editor – nothing fancy. Created a new file, `quicksort.c`. I knew I’d need a standard C setup. So, I started with the basics:
c
#include
// Function prototypes would go here later
void quickSort(int arr[], int low, int high);
int partition(int arr[], int low, int high);
void swap(int a, int b);
void printArray(int arr[], int size);
int main() {
// I’ll put my test array and function calls here
printf(“Starting the quick sort journey…n”);
int data[] = {8, 7, 2, 1, 0, 9, 6};
int n = sizeof(data) / sizeof(data[0]);
printf(“Original array: n”);
printArray(data, n);
// The main call
quickSort(data, 0, n – 1);
printf(“Sorted array: n”);
printArray(data, n);
return 0;

// Need to implement the helper functions down here
Just setting up the `main` function felt like progress. I decided to add `printArray` and `swap` helpers right away because I knew I’d need them. Makes life easier than writing that logic inline everywhere.
c
// Simple swap function
void swap(int a, int b) {
int temp = a;
a = b;
b = temp;
// Function to print an array
void printArray(int arr[], int size) {

for (int i = 0; i < size; ++i) {
printf(“%d “, arr[i]);
printf(“n”);
Tackling the Logic: Partitioning
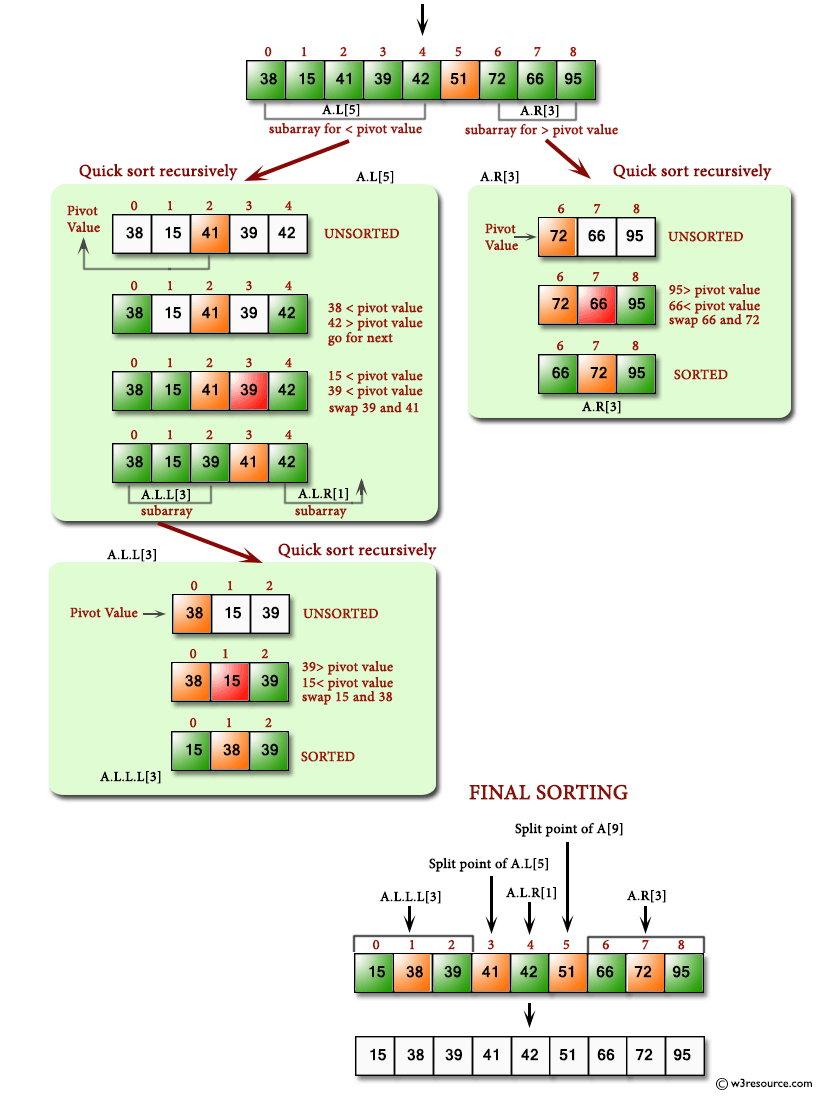
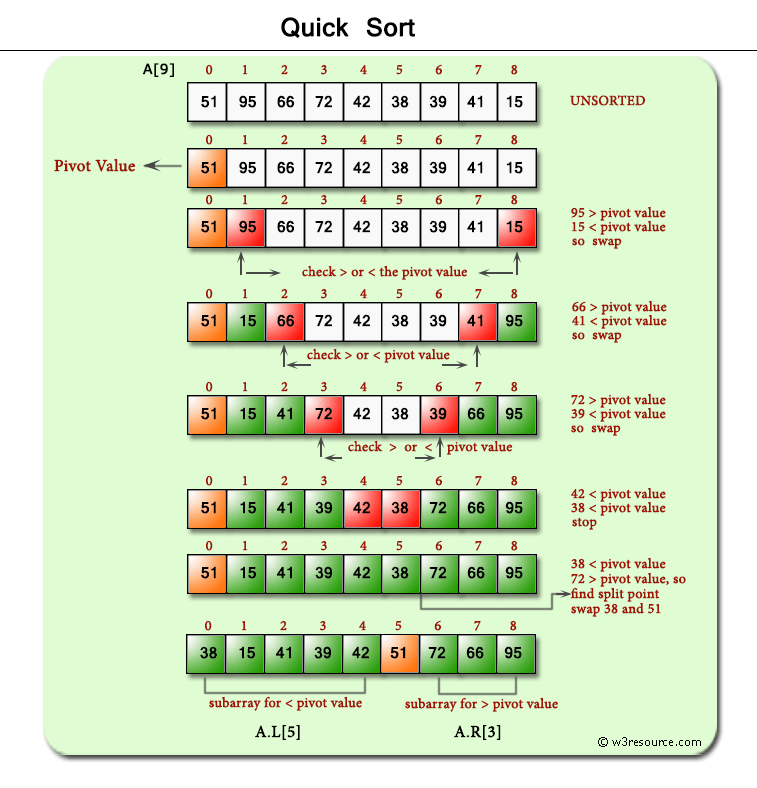
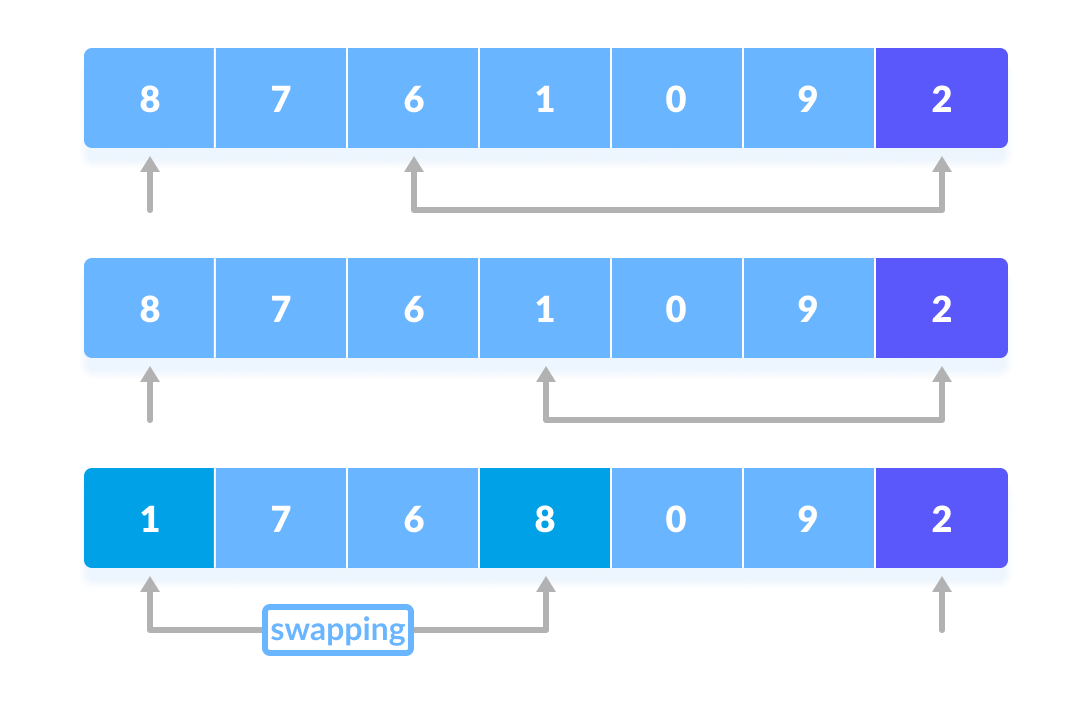
Right, the core of quick sort is this `partition` thing. The idea, as I remembered it, was pick an element (the pivot – I just went with the last element, seemed easiest for a start) and then shuffle things around so all elements smaller than the pivot are before it, and all elements greater are after it. Then you find out where the pivot ended up.
So, I started coding the `partition` function. I needed to keep track of the index for the ‘smaller element’ boundary. Let’s call it `i`.
c
int partition(int arr[], int low, int high) {
// Choosing the last element as pivot
int pivot = arr[high];
// Index of smaller element
int i = (low – 1);
// Loop through elements from low to high-1
for (int j = low; j < high; j++) {
// If current element is smaller than the pivot
if (arr[j] < pivot) {
i++; // Increment index of smaller element
swap(&arr[i], &arr[j]); // Swap it!
// After the loop, swap the pivot (arr[high]) into its correct place
swap(&arr[i + 1], &arr[high]);
// Return the partition index
return (i + 1);
Getting the indices `i` and `j` right, and remembering to swap the pivot into its final place after the loop, took a moment of thinking. Had to trace it mentally with a small example like `[3, 1, 4, 2]` to make sure the swaps made sense.
The Recursive Part: `quickSort`
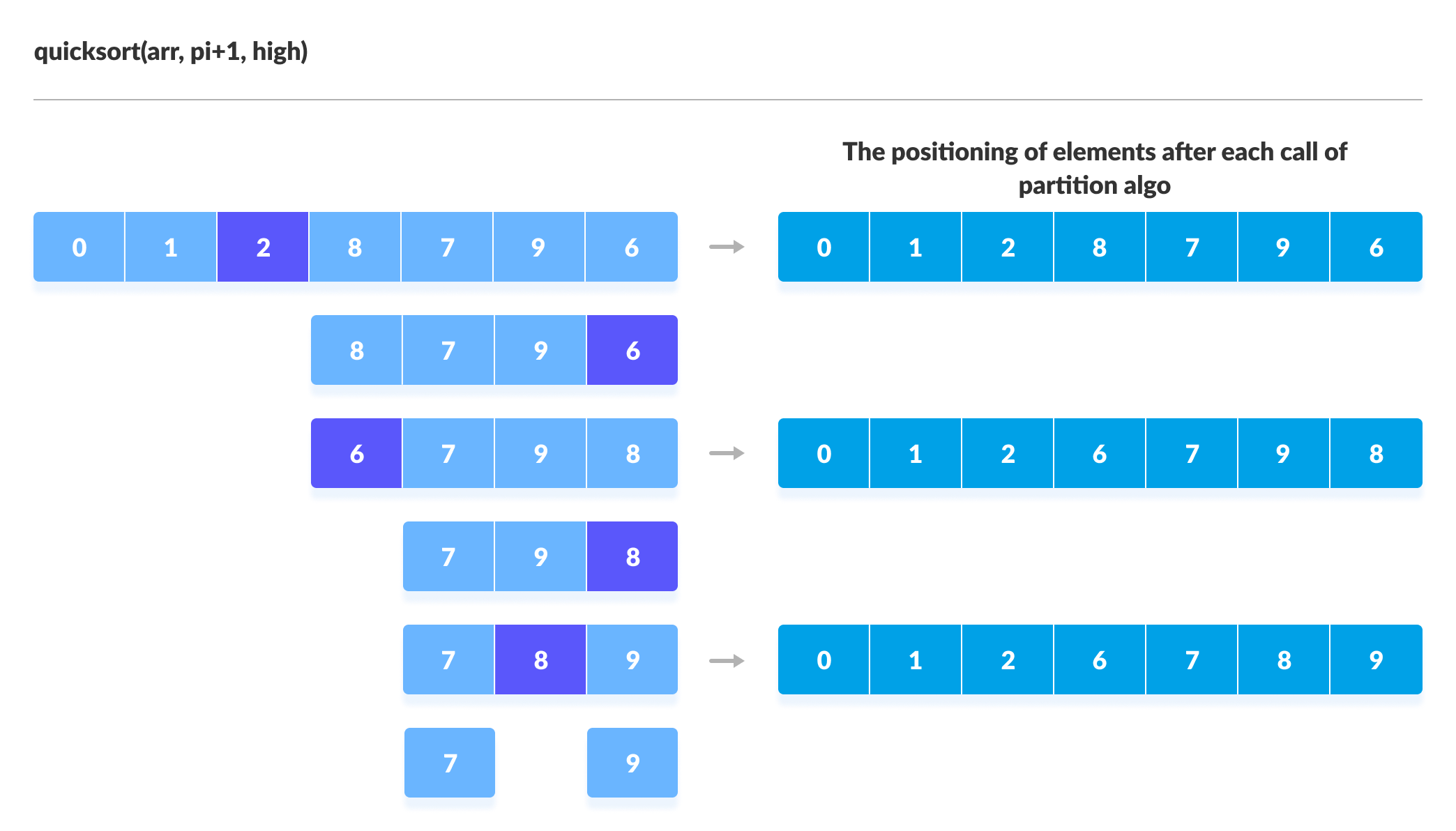
Once `partition` seemed okay, the `quickSort` function itself felt more straightforward. It’s recursive. You partition the array, get the pivot’s final position (`pi`), and then recursively call `quickSort` on the two sub-arrays: the one before the pivot and the one after the pivot.
Crucially, I needed a base case to stop the recursion. That’s when `low` is greater than or equal to `high`, meaning the sub-array has zero or one element, which is already sorted.
c
void quickSort(int arr[], int low, int high) {
if (low < high) {
// pi is partitioning index, arr[pi] is now at right place
int pi = partition(arr, low, high);
// Separately sort elements before partition and after partition
quickSort(arr, low, pi – 1);
quickSort(arr, pi + 1, high);
This recursive structure is pretty elegant once you see it laid out. You break the problem down, solve the smaller pieces, and it comes together.
Testing and Seeing it Run
With all the pieces in place, it was time to compile and run. I used `gcc quicksort.c -o quicksort` in the terminal, then ran `./quicksort`.
Seeing the output:

Starting the quick sort journey…
Original array:
8 7 2 1 0 9 6
Sorted array:
0 1 2 6 7 8 9
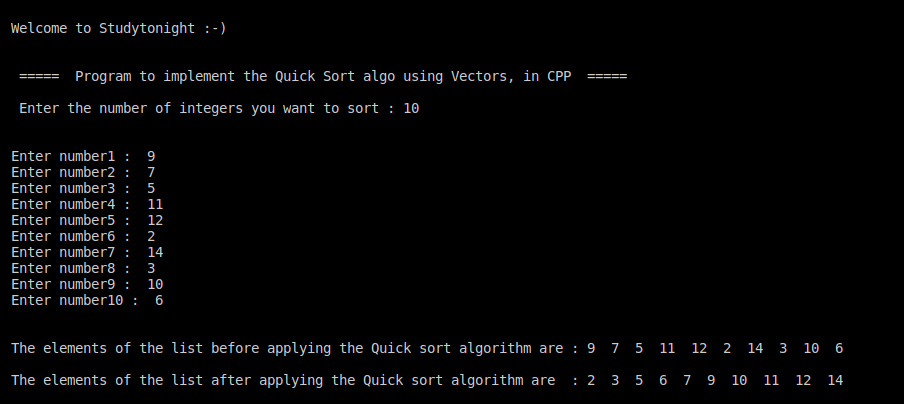
Yes! It worked on the first try with my test data. That felt good. It wasn’t super complex code, but getting sorting algorithms right always gives a little satisfaction. I tried a couple more test cases, like an already sorted array and one with duplicates, just to be sure.
Final Thoughts
So, was it an “easy program”? Well, the C code itself isn’t terribly long. Understanding the partitioning logic is the main hurdle. Once you get that, the recursive part follows naturally. For someone comfortable with C basics (pointers, arrays, functions) and recursion, it’s definitely achievable. It took a bit of focused thinking, especially around the `partition` indices, but overall, a satisfying little coding session. Definitely a good exercise to keep the C skills sharp.
